Solving the “Two Sum” Problem in JavaScript

Photo by Ben Wicks on Unsplash

Algorithm design plays a crucial role in coding interviews, especially for software engineering roles. While some companies place more emphasis on algorithmic challenges than others, they are particularly important for larger tech companies like Google, Facebook, and Amazon. Even though solving algorithm problems during an interview may not fully represent your day-to-day performance as an engineer or predict long-term career success, it’s essential to prepare thoroughly.

To succeed, you must practice regularly, familiarize yourself with common patterns and principles, and be able to articulate the efficiency and trade-offs of your solutions. Understanding how to approach these problems, explain your reasoning, and discuss time and space complexities is a key component of standing out in competitive technical interviews.

The “Two Sum” Problem on LeetCode in JavaScript

The Two Sum problem is one of the most popular coding interview questions and is a great introduction to working with arrays, hashing, and optimization in algorithms. The problem is defined as follows:

Problem Description

Given an array of integers nums and an integer target, return indices of the two numbers such that they add up to target. You may assume that each input would have exactly one solution, and you may not use the same element twice. You can return the answer in any order.

Solving the Two Sum Problem Using Brute Force

Building a Mental Model for the Brute Force Solution

There are multiple ways to solve the Two Sum problem, but the most optimal solution involves using a hash map (or an object in JavaScript) to track the indices of the elements we’ve seen so far, allowing us to check for the complement of each number efficiently. We’ll walk through this solution as well as the brute force solution for comparison.

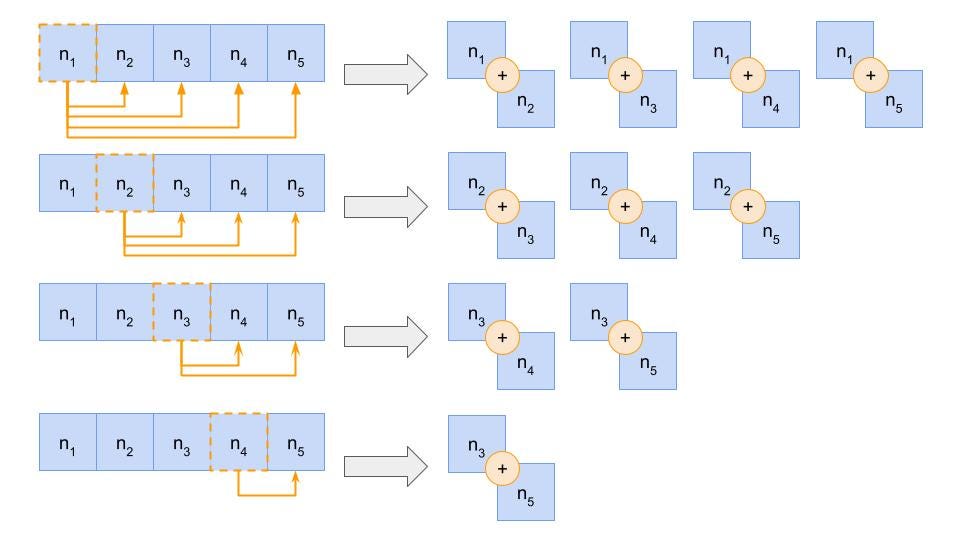
A diagram illustrating a brute force method to solving the Two Sum problem

Much like all brute force method solutions, this implementation indiscriminately iterates through every number pair combination. At each iteration, the sum of each pair will be checked to see if it equals target, and if it does, the algorithm should return the indices of those two numbers.

The idea is simple enough, so let’s take a look at an JavaScript implementation of this solution.

A JavaScript Implementation of a Brute Force Solution to the Two Sum Problem

Let’s walk through the code. In this implementation, I chose to use for loops to iterate through the array of numbers. While it may be considered more idiomatic to use array methods like array.prototype.forEach here, the 2nd loop in this case is looping through a smaller and smaller subset of the original nums array each iteration. This means that I would need to perform some operation on the array to shorten it on each step, or I would need to iterate through the entire array in the second loop. Both of these add time complexity.

Note that you could potentially break out of the nested forEach calls by throwing an exception, but I would argue that is more complex and difficult to understand than the for loop solution, and therefore defeats one the main purposes of idiomatic programming.

Time and Space Complexity of the Brute Force Solution

With regards to time complexity, this solution is considered O(n²) because it the typical and worst-case scenarios, the algorithm needs to iterate through the length of the nums array in a nested fashion. Even if our target pair is found midway through the array, as n approaches infinity, n / 2 is still infinity. While this is definitely a brute force solution, one benefit of this solution is that its space complexity is constant, or O(1).

Solving the Two Sum Problem Optimized for Time

Now, that we’ve worked through the brute force solution, let’s examine an optimization to speed up the algorithm. If you’re in an interview and you have time left after solving a toy problem, your interviewer will sometimes ask you if there is a more efficient way to implement your algorithm. It’s always a good idea to be prepared to discuss the efficiency of your solution and the possibility of making it better.

Building a Mental Model for the Optimized Solution

Here, our mental model requires us to visualize how our map works. On each iteration through our array, we do a lookup on our map for the matching value needed to sum to our target value. If it doesn’t exist, we’ll add the current value and its index to the map, and continue on with the next array iteration. We continue this process until we find a matching sum. When we find it, we return the corresponding indices.

A JavaScript Implementation of a Brute Force Solution to the Two Sum Problem

Let’s analyze the JavaScript implementation to make sure all of the details are clear.

1. Create a map object that we can use to map values to indices. As described previously, we’ll use this to track which values we’ve already encountered.

2. Iterate through the array, and for each number, compute the “complement” (target — num). The compliment is the value needed to pair with the current number so that the sum equals the target.

3. Check if the complement exists in the map. If it does exist, return the current index and the stored index of the complement. However, if it doesn’t exist, add the current number and its index in the map for future reference.

4. Continue this process until you find the pair.

Time and Space Complexity of the Optimized Solution

This approach leverages the efficiency of hash maps, allowing us to solve the problem in one pass through the array and reducing the time complexity of our algorithm to O(n).

However, this improved time efficiency comes at a cost. Since we are storing a reference to the current index for every iteration that doesn’t produce a match, we are increasing our space complexity to O(n), or linear.

Edge Cases to Consider

Whether working on production code or solving toy problems during an interview, it’s always important to handle edge cases.

1. If no solution exists
   The problem explicitly states that there is always exactly one solution, so we don’t need to handle the case of no solution. However, if this weren’t guaranteed, you should consider handling that scenario. This type of variation might be incorporated in an interview.

2. Negative numbers and zeroes
   The algorithm handles negative numbers and zeroes naturally since it treats all integers the same when calculating the complement.

3. Duplicate numbers
   If the array contains duplicate numbers, the algorithm will still function correctly as it tracks indices, not just values. Keep in mind, it will report the first occurrence of the solution.

Variants of the Two Sum Problem

The Two Sum problem has several common variants, each of which requires slight modifications to the approach. Below are some examples you should consider practicing, or at the vary least, conceptualize how you would solve them as a thought exercise.

1. Two Sum With the Input Array Sorted
   In this variant, the input array is already sorted, allowing us to use a two-pointer technique to reduce the space complexity to O(1) while maintaining the linear time complexity.

2. Three Sum
   Here, the task is to find three numbers in the array that add up to a target. This can be solved using nested loops like our brute force scenario or a two-pointer technique that can obtain O(n²) time complexity.

3. Four Sum
   Similar to the Three Sum problem, the Four Sum problem can be solved using the same techniques. The time complexity for the optimal solution is O(n³).

4. Two Sum Less Than K
   Instead of finding an exact sum, this variant asks for the pair whose sum is the largest but less than a given target K. It can also be solved using sorting and a two-pointer approach.

When To Use Brute Force Versus the Optimized Solution

Ultimately, deciding which approach to use depends on your specific scenario. If you’re developing a solution in a real-world, production application, you should consider the bounds of your problem. How large can n be? Is speed critical in this feature or are will this algorithm run in the background? Does the elegant solution compromise readability for your other developers that may need to work on your code in the future?

Most frequently, however, you’ll only encounter this particular challenge in a contrived environment like an interview. In this case, do what you feel confident in completing in the short timeframe that you have. If you don’t feel comfortable implementing the time-optimized solution, state that to your interviewer. Complete the brute force solution and explain that you believe you can optimize that solution to reduce time complexity by tracking the values you’ve already iterated through. This will go a long way with your interviewer.

Conclusion

The Two Sum problem, like many toy problems, can be solved in multiple ways. It’s worthwhile to try implementing a brute force solution as well as a more optimized one. Trading off space efficiency for time efficiency is a common practice in toy problems and in production code, so familiarizing yourself with the practice will set you up for success.

If you enjoyed these explanations and diagrams check out some more posts where I break down toy problems:

• Coding Interviews: Solving the “Palindrome Permutation” Problem in JavaScript

• Coding Interviews: Solving the “Rotate a Matrix” Problem in JavaScript

• Coding Interviews: Solving the “Reverse a Linked List in Place” Problem in JavaScript

Or if you’re looking to learn more about data structures, check out these:

• How to Build a Hash Table in JavaScript

• How to Build a Binary Search Tree in JavaScript

• How to Build a Linked List in JavaScript