Table of contents
- The “Longest Increasing Subsequence” Problem on LeetCode in JavaScript
- Solving the Longest Increasing Subsequence Problem Using A Brute Force Approach
- Solving the Longest Increasing Subsequence Problem Using An Optimized Approach
- Edge Cases to Consider
- Variants of the Number of Islands Problem
- When To Use Brute Force Versus an Optimized Solution
- Conclusion
Photo by Thomas Serer on Unsplash
Tackling algorithmic challenges is a crucial part of coding interviews, particularly for software engineering roles at top tech companies such as Google, Meta, and Amazon. Although these problems may not represent the daily tasks of an engineer, or reliably forecast long-term performance, thorough preparation remains essential.
Regular practice, familiarity with common problem-solving strategies, and the ability to explain the pros and cons of your solutions are vital for securing job offers in a competitive market or being accepted into a respected coding bootcamp. Mastering time and space complexity analysis, and clearly communicating your approach will set you apart in these evaluations.
The “Longest Increasing Subsequence” Problem on LeetCode in JavaScript
The Longest Increasing Subsequence problem on LeetCode says that: given an integer array nums, return the length of the longest strictly increasing subsequence. In this instance, a subsequence is an array that can be derived from another array by deleting zero or more elements without changing the order of the remaining elements.
For example, given the array [10, 9, 2, 5, 3, 7, 101, 18], one of the longest increasing subsequences is [2, 3, 7, 101], and the length of this subsequence is 4.
Solving the Longest Increasing Subsequence Problem Using A Brute Force Approach
The first approach that comes to mind is an iterative, dynamic programming solution where we compare each element with all previous elements. If the current element is larger than a previous one, it might contribute to forming a longer subsequence. We’ll keep track of the length of the longest increasing subsequence that ends at each index of the given array, and after we finish iterating through every possible subsequence, we’ll circle back and report the length of the largest one we found.
Building a Mental Model for the Brute Force Approach
Sometimes building a mental model for dynamic programming algorithms can be a little difficult. Let’s take a look at a visual representation to make this algorithm more mentally digestible.
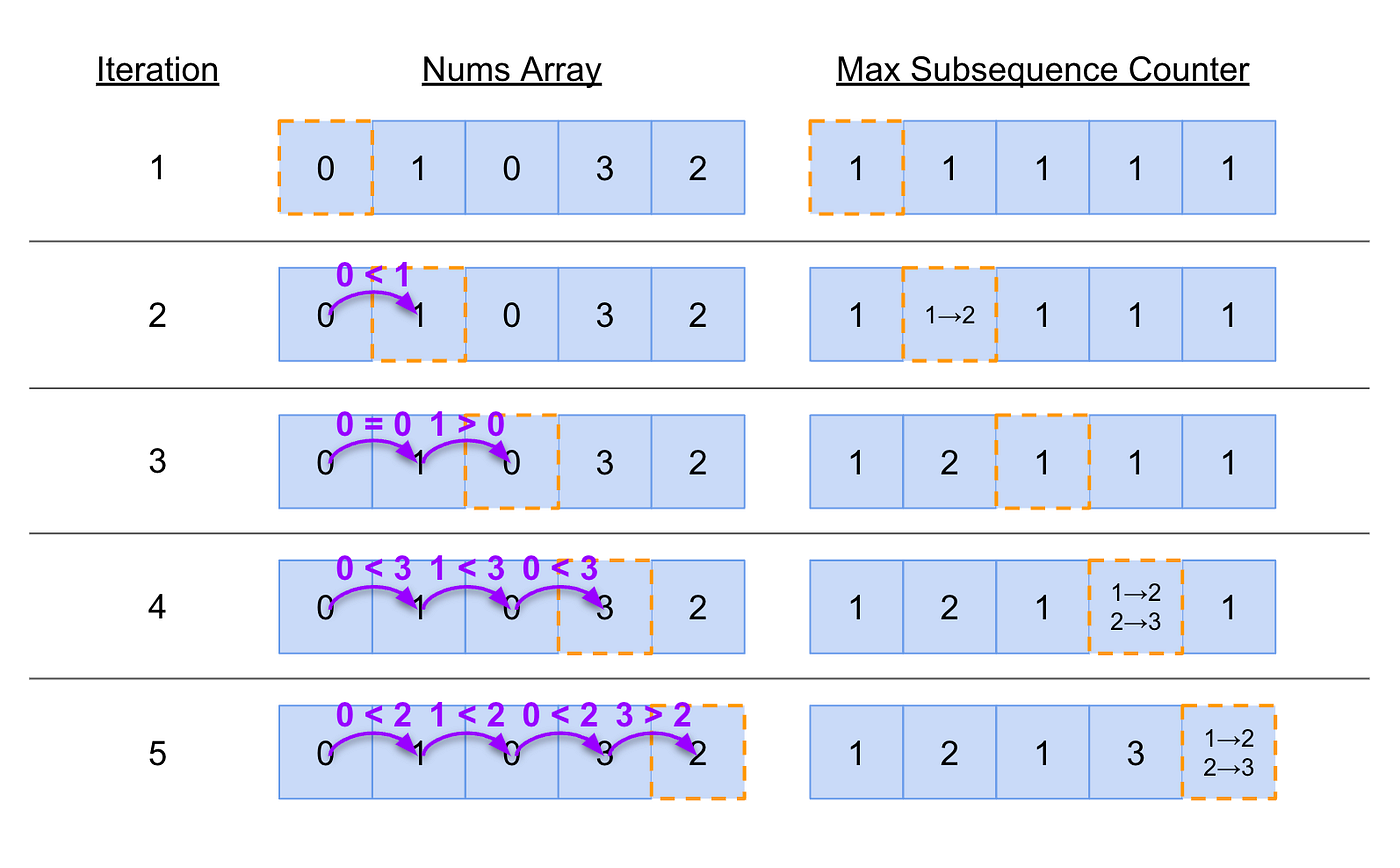
A visual representation of a brute force approach to solving the Longest Increasing Subsequence problem
A JavaScript Implementation of a Brute Force Solution to the Longest Increasing Subsequence Problem
Now that our mental model is solidified, let’s see what this looks like in code. I always recommend working through a mental model prior to coding because it removes a layer of complexity while you’re designing your algorithm.
function lengthOfLIS(nums) {
if (nums.length === 0) return 0;
const maxSubsequenceLengths = new Array(nums.length).fill(1);
for (let i = 1; i < nums.length; i++) {
for (let j = 0; j < i; j++) {
if (nums[i] > nums[j]) {
const currentMax = maxSubsequenceLengths[i];
const newMaxCandidate = maxSubsequenceLengths[j] + 1;
maxSubsequenceLengths[i] = Math.max(
currentMax,
newMaxCandidate
);
}
}
}
return Math.max(...maxSubsequenceLengths);
}
Handle empty array:
Our base algorithm isn’t set up to handle an emptynumsarray parameter, so we’ll add theifstatement at the beginning of the function to short-circuit the algorithm and return0.Initialize our maximum subsequence counter:
Here, we instantiate a new array with a length that matches the length of the incomingnumsarray. Then, we fill it with1values so as to initialize every maximum subsequence length to be1—the smallest possible subsequence length.Setting up the iteration parameters:
In this part of the algorithm, we set up our loops such that we iterate through the entirenumsarray, and for each step in that loop, we also march through each item in the array from index 0 up to the current item in the array. So, for each subsequent step in the outer loop, we’re iterating through a large subset of the array.Conditionally updating the maximum subsequence counter:
This is the heart of the algorithm and potentially the most important. We check if the current item from the outer loop is greater than the current item from the inner loop. If so, we know that the longest subsequence is at least as long as one more than the longest subsequence that was possible at the inner loop index. Let that sink in. If the current value is larger than the value at the inner loop index, that means that we can add the new value onto the longest subsequence at the inner loop index. After, we’ll update our counter at that index to be the larger of the existing value there and the length of the subsequence we just calculated.Final results:
Finally, we can find the largest subsequence length in our counter array and return that.
Time and Space Complexity
This solution has a time complexity of O(n²) where n is the number of elements in the input array nums. This is because we have a nested loop: the outer loop runs through each element, and the inner loop compares it with all previous elements.
Solving the Longest Increasing Subsequence Problem Using An Optimized Approach
Although the dynamic programming approach works, there’s an even more optimized solution using a combination of binary search and dynamic programming that can bring the time complexity down even further.
Use a helper array (sub) that will store the smallest possible tail value for increasing subsequences of different lengths. For each element in nums, use binary search to find its position in the sub array and either replace an existing value or append the new value, ensuring that sub always remains sorted.
Building a Mental Model for the Optimized Approach
Again, building a mental model is important step in algorithm design, so we’ll build one in a similar style to prior one so we can compare.
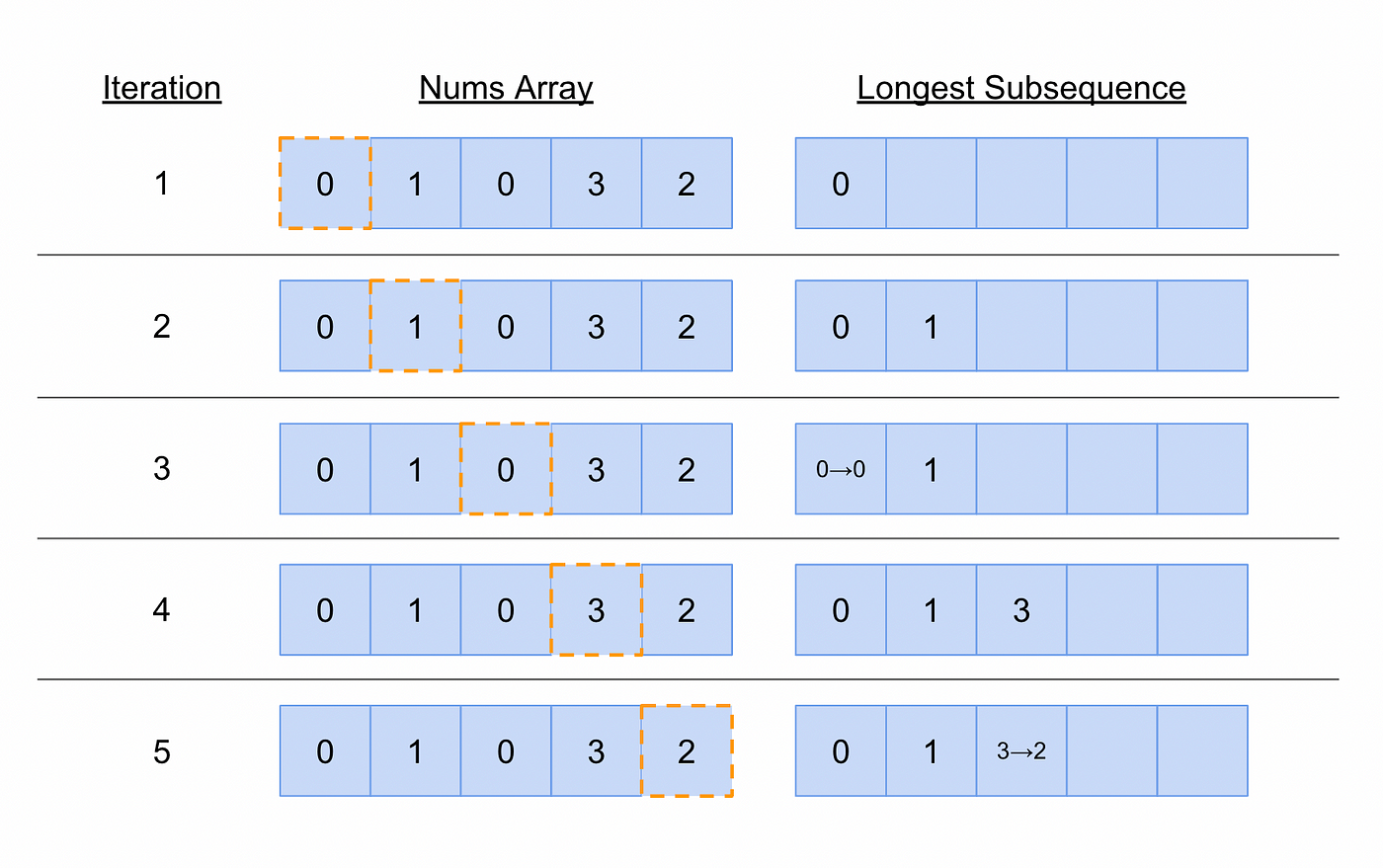
A JavaScript Implementation of an Optimized Solution to the Longest Increasing Subsequence Problem
Admittedly, it’s a little difficult to illustrate the entire algorithm in our mental model diagram. While we could have easily added the binary search portion of the routine to the illustration, it might have reduced overall clarity and been counterproductive. Instead, let’s look at the code and we’ll address the binary search routine below.
function lengthOfLIS(nums) {
const sub = [];
for (let num of nums) {
// Find the position of 'num' in the sub array using binary search
let left = 0, right = sub.length;
while (left < right) {
let mid = Math.floor((left + right) / 2);
if (sub[mid] < num) {
left = mid + 1;
} else {
right = mid;
}
}
// If 'num' is larger than any element in sub, append it to the end
// Otherwise, replace the element at position 'left'
if (left >= sub.length) {
sub.push(num);
} else {
sub[left] = num;
}
}
return sub.length;
}
subarray
We’ll instantiate an array to store our ongoing longest increasing subsequence. As an aside, you’ll notice we instantiate the array using theconstkeyword instead ofletorvar. Although, we’ll push items into the array and potentially overwrite items as we go along, we’ll never reassign the variable, and therefore, we can useconstfor a bit of static testing.forloop
This may seem a bit obvious, but there’s no way around iterating through the entire array. Because each subsequent item in the array could be larger in value, we’ll need to check every single item.whileloop
In order to optimize the runtime of this algorithm, we can’t use nestedforloops like in our brute force approach. Instead, our inner loop will be awhileloop that implements a binary search to find where the currentnumvalue would be sorted into oursubarray. Because our binary search eliminates half of the items from consideration on each iteration, ourwhileloop will be less thanO(n)time complexity.numplacement
This is where the magic happens. Thesubarray keeps track of potential end values of increasing subsequences of different lengths, and by replacing the values using binary search, we efficiently find the best place for each element in the subsequence. This ensures that we are able to maintain a valid increasing subsequence while reducing the overall complexity.
Time and Space Complexity
Time Complexity
Because a binary search is performed onnelements, the time complexity of this algorithm isO(n x log n). That is to say, for allnelements of thenumsarray, we perform anO(log n)operation, and therefore, the total time complexity becomesO(n x log n).Space Complexity
Similarly to the brute force approach, the space complexity isO(n)because we store information of lengthn—the same length as thenumsarray.
Edge Cases to Consider
Empty Array
When thenumsarray is empty (i.e. has a length of0), the algorithm should return0. Our algorithms handle this by initializing thesubarray as an empty array and returning the length of that array.All Array Items Are Equal
In the event that all items in thenumsarray for equal (e.g.[7, 7, 7, 7]), the algorithm needs produce1, since that is the longest subsequence.Array Contains Negative Numbers
Negative numbers are valid, and the algorithm should handle them correctly.
Variants of the Number of Islands Problem
Length of the longest decreasing subsequence
Exactly as it sounds, this variant asks you to find the longest decreasing subsequence instead of increasing.Find the longest increasing subsequence itself, not just the length
In this case, the brute force approach will not work and you will need to track the actual subsequence like in the optimized approach.
When To Use Brute Force Versus an Optimized Solution
When solving the Longest Increasing Subsequence problem, the choice between the brute force solution and the optimized solution depends on the context, including the input size, performance constraints, and whether the goal is simply to understand the problem or to solve it efficiently. For large input arrays or where performance is critical, implementing the optimized solution makes sense. If performance isn’t critical and simplicity and clarity are more important, using the brute force solution may be advantageous.
Conclusion
We’ve covered two approaches to solving the “Longest Increasing Subsequence” problem: the dynamic programming solution with a time complexity of O(n²) and the optimized binary search approach that reduced the time complexity to O(n x log n). Both of these approaches use similar memory (O(n)), but which approach you choose depends on your specific scenario. If you’re asked this question in an interview or any other high-pressure scenario, implement the solution that you’re most comfortable with. Happy coding!
